Modeling in NLPy¶
Using Models in the AMPL Modeling Language¶
The amplpy Module¶
Python interface to the AMPL modeling language
- class amplpy.AmplModel(model, **kwargs)¶
Bases: nlpy.model.nlp.NLPModel
AmplModel creates an instance of an AMPL model. If the nl file is already available, simply call AmplModel(stub) where the string stub is the name of the model. For instance: AmplModel(‘elec’). If only the .mod file is available, set the positional parameter neednl to True so AMPL generates the nl file, as in AmplModel(‘elec.mod’, data=’elec.dat’, neednl=True).
- A(*args)¶
Evaluate sparse Jacobian of the linear part of the constraints. Useful to obtain constraint matrix when problem is a linear programming problem.
- AtOptimality(x, y, z, **kwargs)¶
See OptimalityResiduals() for a description of the arguments.
Returns: res: tuple of residuals, as returned by OptimalityResiduals(), optimal: True if the residuals fall below the thresholds specified by self.stop_d, self.stop_c and self.stop_p.
- OptimalityResiduals(x, y, z, **kwargs)¶
Evaluate the KKT or Fritz-John residuals at (x, y, z). The sign of the objective gradient is adjusted in this method as if the problem were a minimization problem.
Parameters : x: Numpy array of length n giving the vector of primal variables, y: Numpy array of length m + nrangeC giving the vector of Lagrange multipliers for general constraints (see below), z: Numpy array of length nbounds + nrangeB giving the vector of Lagrange multipliers for simple bounds (see below). Keywords : c: constraints vector, if known. Must be in appropriate order (see below). g: objective gradient, if known. J: constraints Jacobian, if known. Must be in appropriate order (see below). Returns: vectors of residuals (dual_feas, compl, bnd_compl, primal_feas, bnd_feas)
The multipliers y associated to general constraints must be ordered as follows:
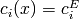 (i in equalC): y[:nequalC]
(i in equalC): y[:nequalC]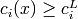 (i in lowerC): y[nequalC:nequalC+nlowerC]
(i in lowerC): y[nequalC:nequalC+nlowerC]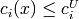 (i in upperC): y[nequalC+nlowerC:nequalC+nlowerC+nupperC]
(i in upperC): y[nequalC+nlowerC:nequalC+nlowerC+nupperC]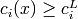 (i in rangeC): y[nlowerC+nupperC:m]
(i in rangeC): y[nlowerC+nupperC:m]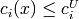 (i in rangeC): y[m:]
(i in rangeC): y[m:]For inequality constraints, the sign of each y[i] should be as if it corresponded to a nonnegativity constraint, i.e.,
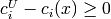 instead of
instead of 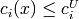 .
.For equality constraints, the sign of each y[i] should be so the Lagrangian may be written:
L(x,y,z) = f(x) - <y, c_E(x)> - ...
Similarly, the multipliers z associated to bound constraints must be ordered as follows:
- x_i = L_i (i in fixedB) : z[:nfixedB]
- x_i geq L_i (i in lowerB) : z[nfixedB:nfixedB+nlowerB]
- x_i leq U_i (i in upperB) : z[nfixedB+nlowerB:nfixedB+nlowerB+nupperB]
- x_i geq L_i (i in rangeB) : z[nfixedB+nlowerB+nupperB:nfixedB+nlowerB+nupperB+nrangeB]
- x_i leq U_i (i in rangeB) : z[nfixedB+nlowerB+nupper+nrangeB:]
The sign of each z[i] should be as if it corresponded to a nonnegativity constraint (except for fixed variables), i.e., those z[i] should be nonnegative.
It is possible to check the Fritz-John conditions via the keyword FJ. If FJ is present, it should be assigned the multiplier value that will be applied to the gradient of the objective function.
Example: OptimalityResiduals(x, y, z, FJ=1.0e-5)
If FJ has value 0.0, the gradient of the objective will not be included in the residuals (it will not be computed).
- ResetCounters()¶
Reset the feval, geval, Heval, Hprod, ceval, Jeval and Jprod counters of the current instance to zero.
- close()¶
- cons(x)¶
Evaluate vector of constraints at x. Returns a Numpy array.
The constraints appear in natural order. To order them as follows
- equalities
- lower bound only
- upper bound only
- range constraints,
use the permC permutation vector.
- consPos(x)¶
Convenience function to return the vector of constraints reformulated as
ci(x) - ai = 0 for i in equalC ci(x) - Li >= 0 for i in lowerC + rangeC Ui - ci(x) >= 0 for i in upperC + rangeC.
The constraints appear in natural order, except for the fact that the ‘upper side’ of range constraints is appended to the list.
- cost()¶
Evaluate sparse cost vector. Useful when problem is a linear program. Return a sparse vector. This method changes the sign of the cost vector if the problem is a maximization problem.
- display_basic_info()¶
Display vital statistics about the current model.
- grad(x)¶
Evaluate objective gradient at x. Returns a Numpy array. This method changes the sign of the objective gradient if the problem is a maximization problem.
- hess(x, z, *args)¶
Evaluate sparse lower triangular Hessian at (x, z). Returns a sparse matrix in format self.mformat (0 = compressed sparse row, 1 = linked list).
Note that the sign of the Hessian matrix of the objective function appears as if the problem were a minimization problem.
- hprod(z, v, **kwargs)¶
Evaluate matrix-vector product H(x,z) * v. Returns a Numpy array.
Note that the sign of the Hessian matrix of the objective function appears as if the problem were a minimization problem.
- icons(i, x)¶
Evaluate value of i-th constraint at x. Returns a floating-point number.
- igrad(i, x)¶
Evaluate dense gradient of i-th constraint at x. Returns a Numpy array.
- irow(i)¶
Evaluate sparse gradient of the linear part of the i-th constraint. Useful to obtain constraint rows when problem is a linear programming problem.
- islp()¶
Determines whether problem is a linear programming problem.
- jac(x, *args)¶
Evaluate sparse Jacobian of constraints at x. Returns a sparse matrix in format self.mformat (0 = compressed sparse row, 1 = linked list).
The constraints appear in the following order:
- equalities
- lower bound only
- upper bound only
- range constraints.
- jacPos(x)¶
Convenience function to evaluate the Jacobian matrix of the constraints reformulated as
ci(x) = ai for i in equalC
ci(x) - Li >= 0 for i in lowerC
ci(x) - Li >= 0 for i in rangeC
Ui - ci(x) >= 0 for i in upperC
Ui - ci(x) >= 0 for i in rangeC.
The gradients of the general constraints appear in ‘natural’ order, i.e., in the order in which they appear in the problem. The gradients of range constraints appear in two places: first in the ‘natural’ location and again after all other general constraints, with a flipped sign to account for the upper bound on those constraints.
The overall Jacobian of the new constraints thus has the form
[ J ] [-JR]
This is a m + nrangeC by n matrix, where J is the Jacobian of the general constraints in the order above in which the sign of the ‘less than’ constraints is flipped, and JR is the Jacobian of the ‘less than’ side of range constraints.
- obj(x)¶
Evaluate objective function value at x. Returns a floating-point number. This method changes the sign of the objective value if the problem is a maximization problem.
- set_x(x)¶
Set x as current value for subsequent calls to obj(), grad(), jac(), etc. If several of obj(), grad(), jac(), ..., will be called with the same argument x, it may be more efficient to first call set_x(x). In AMPL, obj(), grad(), etc., normally check whether their argument has changed since the last call. Calling set_x() skips this check.
See also unset_x().
- sgrad(x)¶
Evaluate sparse objective gradient at x. Returns a sparse vector. This method changes the sign of the objective gradient if the problem is a maximization problem.
- sigrad(i, x)¶
Evaluate sparse gradient of i-th constraint at x. Returns a sparse vector representing the sparse gradient in coordinate format.
- unset_x()¶
Reinstates the default behavior of obj(), grad(), jac, etc., which is to check whether their argument has changed since the last call.
See also set_x().
- writesol(x, z, msg)¶
Write primal-dual solution and message msg to stub.sol
Example¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 | #!/usr/bin/env python
#
# Test for amplpy module
#
from nlpy.model import AmplModel
import numpy
import getopt, sys
PROGNAME = sys.argv[0]
def commandline_err( msg ):
sys.stderr.write( "%s: %s\n" % ( PROGNAME, msg ) )
sys.exit( 1 )
def parse_cmdline( arglist ):
if len( arglist ) != 1:
commandline_err( 'Specify file name (look in data directory)' )
return None
try: options, fname = getopt.getopt( arglist, '' )
except getopt.error, e:
commandline_err( "%s" % str( e ) )
return None
return fname[0]
ProblemName = parse_cmdline(sys.argv[1:])
# Create a model
print 'Problem', ProblemName
nlp = AmplModel( ProblemName ) #amplpy.AmplModel( ProblemName )
# Query the model
x0 = nlp.x0
pi0 = nlp.pi0
n = nlp.n
m = nlp.m
print 'There are %d variables and %d constraints' % ( n, m )
max_n = min( n, 5 )
max_m = min( m, 5 )
print
print ' Printing at most 5 first components of vectors'
print
print 'Initial point: ', x0[:max_n]
print 'Lower bounds on x: ', nlp.Lvar[:max_n]
print 'Upper bounds on x: ', nlp.Uvar[:max_n]
print 'f( x0 ) = ', nlp.obj( x0 )
g0 = nlp.grad( x0 )
print 'grad f( x0 ) = ', g0[:max_n]
if max_m > 0:
print 'Initial multipliers: ', pi0[:max_m]
print 'Lower constraint bounds: ', nlp.Lcon[:max_m]
print 'Upper constraint bounds: ', nlp.Ucon[:max_m]
c0 = nlp.cons( x0 )
print 'c( x0 ) = ', c0[:max_m]
J = nlp.jac( x0 )
H = nlp.hess( x0, pi0 )
print
print ' nnzJ = ', J.nnz
print ' nnzH = ', H.nnz
print
print ' Printing at most first 5x5 principal submatrix'
print
print 'J( x0 ) = ', J[:max_m,:max_n]
print 'Hessian (lower triangle):', H[:max_n,:max_n]
print
print ' Evaluating constraints individually, sparse gradients'
print
for i in range(max_m):
ci = nlp.icons( i, x0 )
print 'c%d( x0 ) = %-g' % (i, ci)
sgi = nlp.sigrad( i, x0 )
k = sgi.keys()
ssgi = {}
for j in range( min( 5, len( k ) ) ):
ssgi[ k[j] ] = sgi[ k[j] ]
print 'grad c%d( x0 ) = ' % i, ssgi
print
print ' Testing matrix-vector product:'
print
e = numpy.ones( n, 'd' )
e[0] = 2
e[1] = -1
He = nlp.hprod( pi0, e )
print 'He = ', He[:max_n]
# Output "solution"
nlp.writesol( x0, pi0, 'And the winner is' )
# Clean-up
nlp.close()
|
Modeling with NLPModel Objects¶
The nlp Module¶
- class nlp.NLPModel(n=0, m=0, name='Generic', **kwargs)¶
Instances of class NLPModel represent an abstract nonlinear optimization problem. It features methods to evaluate the objective and constraint functions, and their derivatives. Instances of the general class do not do anything interesting; they must be subclassed and specialized.
Parameters : n: number of variables (default: 0) m: number of general (non bound) constraints (default: 0) name: model name (default: ‘Generic’) Keywords : x0: initial point (default: all 0) pi0: vector of initial multipliers (default: all 0) Lvar: vector of lower bounds on the variables (default: all -Infinity) Uvar: vector of upper bounds on the variables (default: all +Infinity) Lcon: vector of lower bounds on the constraints (default: all -Infinity) Ucon: vector of upper bounds on the constraints (default: all +Infinity) Constraints are classified into 3 classes: linear, nonlinear and network.
Indices of linear constraints are found in member lin (default: empty).
Indices of nonlinear constraints are found in member nln (default: all).
Indices of network constraints are found in member net (default: empty).
If necessary, additional arguments may be passed in kwargs.
- AtOptimality(x, z, **kwargs)¶
- OptimalityResiduals(x, z, **kwargs)¶
- ResetCounters()¶
- cons(x, **kwargs)¶
- grad(x, **kwargs)¶
- hess(x, z, **kwargs)¶
- hprod(x, z, p, **kwargs)¶
- icons(i, x, **kwargs)¶
- igrad(i, x, **kwargs)¶
- jac(x, **kwargs)¶
- obj(x, **kwargs)¶
- sigrad(i, x, **kwargs)¶
Example¶
Todo
Insert example.
Using the Slack Formulation of a Model¶
The slacks Module¶
A framework for converting a general nonlinear program into a farm with (possibly nonlinear) equality constraints and bounds only, by adding slack variables.
SlackFramework is a general framework for converting a nonlinear optimization problem to a form using slack variables.
The initial problem consists in minimizing an objective 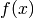 subject to
the constraints
subject to
the constraints
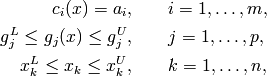
where some or all lower bounds 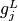 and
and 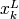 may be equal to
may be equal to
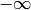 , and some or all upper bounds
, and some or all upper bounds 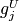 and
and 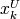 may be equal to
may be equal to 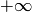 .
.
The transformed problem is in the variables x, s and t and its constraints have the form
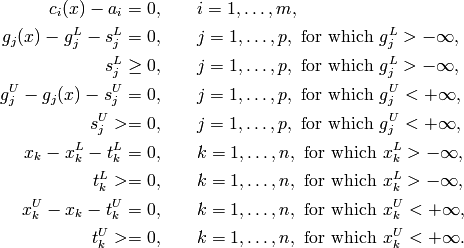
In the latter problem, the only inequality constraints are bounds on the slack variables. The other constraints are (typically) nonlinear equalities.
The order of variables in the transformed problem is as follows:
[ x | sL | sU | tL | tU ]
where:
- sL = [ sLL | sLR ], sLL being the slack variables corresponding to general constraints with a lower bound only, and sLR being the slack variables corresponding to the ‘lower’ side of range constraints.
- sU = [ sUU | sUR ], sUU being the slack variables corresponding to general constraints with an upper bound only, and sUR being the slack variables corresponding to the ‘upper’ side of range constraints.
- tL = [ tLL | tLR ], tLL being the slack variables corresponding to variables with a lower bound only, and tLR being the slack variables corresponding to the ‘lower’ side of two-sided bounds.
- tU = [ tUU | tUR ], tUU being the slack variables corresponding to variables with an upper bound only, and tLR being the slack variables corresponding to the ‘upper’ side of two-sided bounds.
This framework initializes the slack variables sL, sU, tL, and tU to zero by default.
Note that the slack framework does not update all members of AmplModel, such as the index set of constraints with an upper bound, etc., but rather performs the evaluations of the constraints for the updated model implicitly.
- class slacks.SlackFramework(model, **kwargs)¶
Bases: nlpy.model.amplpy.AmplModel
General framework for converting a nonlinear optimization problem to a form using slack variables.
In the latter problem, the only inequality constraints are bounds on the slack variables. The other constraints are (typically) nonlinear equalities.
The order of variables in the transformed problem is as follows:
- x, the original problem variables.
- sL = [ sLL | sLR ], sLL being the slack variables corresponding to general constraints with a lower bound only, and sLR being the slack variables corresponding to the ‘lower’ side of range constraints.
- sU = [ sUU | sUR ], sUU being the slack variables corresponding to general constraints with an upper bound only, and sUR being the slack variables corresponding to the ‘upper’ side of range constraints.
- tL = [ tLL | tLR ], tLL being the slack variables corresponding to variables with a lower bound only, and tLR being the slack variables corresponding to the ‘lower’ side of two-sided bounds.
- tU = [ tUU | tUR ], tUU being the slack variables corresponding to variables with an upper bound only, and tLR being the slack variables corresponding to the ‘upper’ side of two-sided bounds.
This framework initializes the slack variables sL, sU, tL, and tU to zero by default.
Note that the slack framework does not update all members of AmplModel, such as the index set of constraints with an upper bound, etc., but rather performs the evaluations of the constraints for the updated model implicitly.
- A()¶
Return the constraint matrix if the problem is a linear program. See the documentation of jac() for more information.
- Bounds(x)¶
Evaluate the vector of equality constraints corresponding to bounds on the variables in the original problem.
- InitializeSlacks(val=0.0, **kwargs)¶
Initialize all slack variables to given value. This method may need to be overridden.
- cons(x)¶
Evaluate the vector of general constraints for the modified problem. Constraints are stored in the order in which they appear in the original problem. If constraint i is a range constraint, c[i] will be the constraint that has the slack on the lower bound on c[i]. The constraint with the slack on the upper bound on c[i] will be stored in position m + k, where k is the position of index i in rangeC, i.e., k=0 iff constraint i is the range constraint that appears first, k=1 iff it appears second, etc.
Constraints appear in the following order:
[ c ] general constraints in origninal order [ cR ] ‘upper’ side of range constraints [ b ] linear constraints corresponding to bounds on original problem [ bR ] linear constraints corresponding to ‘upper’ side of two-sided
bounds
- jac(x)¶
Evaluate the Jacobian matrix of all equality constraints of the transformed problem. The gradients of the general constraints appear in ‘natural’ order, i.e., in the order in which they appear in the problem. The gradients of range constraints appear in two places: first in the ‘natural’ location and again after all other general constraints, with a flipped sign to account for the upper bound on those constraints.
The gradients of the linear equalities corresponding to bounds on the original variables appear in the following order:
- variables with a lower bound only
- lower bound on variables with two-sided bounds
- variables with an upper bound only
- upper bound on variables with two-sided bounds
The overall Jacobian of the new constraints thus has the form:
[ J -I ] [-JR -I ] [ I -I ] [-I -I]
where the columns correspond, in order, to the variables x, s, sU, t, and tU, the rows correspond, in order, to
- general constraints (in natural order)
- ‘upper’ side of range constraints
- bounds, ordered as explained above
- ‘upper’ side of two-sided bounds,
and where the signs corresponding to ‘upper’ constraints and upper bounds are flipped in the (1,1) and (3,1) blocks.
- obj(x)¶
Example¶
Todo
Insert example.